外观
机器学习
约 6890 字大约 23 分钟
人工智能相关概念
人工智能
人工智能 (AI) 是一组使计算机能够模拟人类智能,从而学习、推理、解决问题、感知环境并执行高级任务(如语言理解、图像识别)的技术。作为计算机科学的一个分支,它通过处理海量数据、应用机器学习和深度学习算法来不断优化,被广泛应用于自动驾驶、医疗诊断和智能助手等各行各业。
核心概览:
- 定义:是指制造智能机器的科学与工程,致力于让计算机模拟人类的学习、判断和行动。
- 三大核心要素:算力、算法、数据。
- 关键分类:
- 弱人工智能 (ANI):专注特定任务的AI(如Apple Siri、AlphaGo、图像识别),是目前普遍应用的类型。
- 通用人工智能 (AGI):具备与人类相当的广泛智慧,能执行任何智能任务。
- 超级人工智能 (ASI):理论上在所有领域远超人类智能的AI。
- 主要子领域:
- 机器学习 (ML):让计算机通过经验和数据自主学习。
- 深度学习 (DL):一种多层神经网络机器学习技术,是当前人工智能突破的主力。
- 自然语言处理 (NLP):实现人机自然语言交流。
- 计算机视觉:赋予机器看和识别物体的能力。
- 当前应用:生成式AI(如ChatGPT生成文本、图像)、自动驾驶汽车、数据分析挖掘、医疗诊断、金融风控等。
人工智能正迅速改变世界,是一项以数据驱动决策并最大化成功机会的变革性技术。
机器学习
机器学习是人工智能的一个分支,向系统输入大量数据后,系统会使用神经网络和深度学习进行自主学习和改进,无需对其明确编程。机器学习可让计算机系统通过累积更多“经验”来不断调整并增强自身功能,因此,通过提供更大、更多样化的数据集进行处理,可以提高这些系统的性能。
深度学习
深度学习(Deep Learning)是机器学习的一个子集,基于多层人工神经网络模拟人脑处理数据,擅长从海量数据中自动学习复杂的非线性特征。它无需人工干预即可进行特征提取(如卷积神经网络 CNN、循环神经网络 RNN),广泛应用于计算机视觉、语音识别和自然语言处理等领域。其核心在于通过隐藏层逐层抽象数据信息。
深度学习的核心原理与特点
- 多层神经网络架构: 深度学习的“深度”是指网络中拥有多个隐藏层,能够层层处理、提取不同级别的特征(从低级边缘到高级物体)。
- 自动化特征工程: 区别于传统机器学习,深度学习能自动从原始数据中学习有效的表征,避免了手动设计特征的繁琐和限制。
- 依赖大数据和大算力: 其性能随数据量增加而提升,处理复杂任务需要强大的计算资源。
常见深度学习模型类型
- 卷积神经网络(CNN): 擅长处理图像和视频数据,通过卷积和池化过滤图片信息。
- 循环神经网络(RNN/LSTM): 专门处理时序数据或序列数据,具备记忆前一层信息的能力。
- 生成对抗网络(GAN): 通过生成器与判别器的博弈提升输出准确率,常用于图像生成。
主要应用领域
- 计算机视觉:人脸识别、物体检测、自动驾驶。
- 语音与自然语言处理:语音转文字、机器翻译、智能对话助手。
- 预测与分析:数据集中的复杂模式分析与见解生成。
深度学习不仅能模拟生物神经网络的运作,更是目前解决强人工智能技术中最具潜力的途径之一。
人工智能中包括机器学习,机器学习中又包括深度学习。
img
机器学习相关概念
| 名称 | 英文 | 所属层级 | 严格定义 | 在数据中的位置 | 主要作用 | 示例 |
|---|---|---|---|---|---|---|
| 样本 | Sample | 行级 | 数据集中的一条独立观测记录 | 一行 | 表示一个研究对象 | 一条用户记录 / 一封邮件 / 一套房 |
| 特征 | Feature | 列级(输入) | 描述样本属性的输入变量 | 多列 | 作为模型输入 | 年龄、面积、点击次数 |
| 标签 | Label / Target | 列级(输出) | 样本对应的真实结果值 | 通常1列 | 作为监督学习的目标 | 是否违约、房价、类别 |
| 训练集 | Training Set | 数据子集 | 用于训练模型参数的数据集合 | 样本子集 | 让模型学习规律 | 用来“拟合”模型 |
| 测试集 | Test Set | 数据子集 | 用于评估模型效果的数据集合 | 样本子集 | 检验泛化能力 | 用来“打分”模型 |
| 学习类型 | 是否需要标签 | 核心目标 | 典型任务 | 输出形式 | 训练方式 |
|---|---|---|---|---|---|
| 有监督学习 | 必须有 | 学习输入→输出映射 | 分类、回归 | 预测值 | 用已知答案训练 |
| 无监督学习 | 不需要 | 发现数据结构 | 聚类、降维 | 结构/分组 | 自动找模式 |
| 半监督学习 | 少量有标签 | 利用未标注数据 | 分类 | 预测值 | 混合训练 |
| 强化学习 | 没有固定标签 | 学习最优策略 | 决策控制 | 动作策略 | 奖励驱动 |
机器学习的建模流程
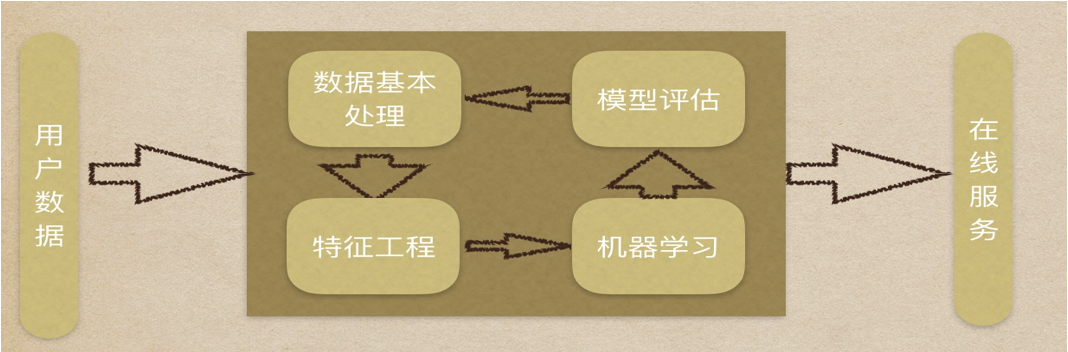
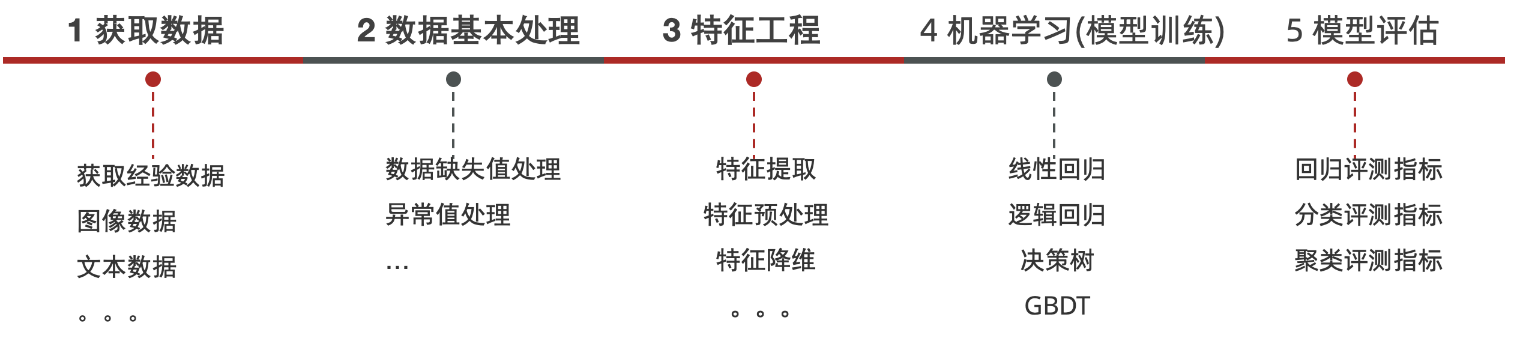
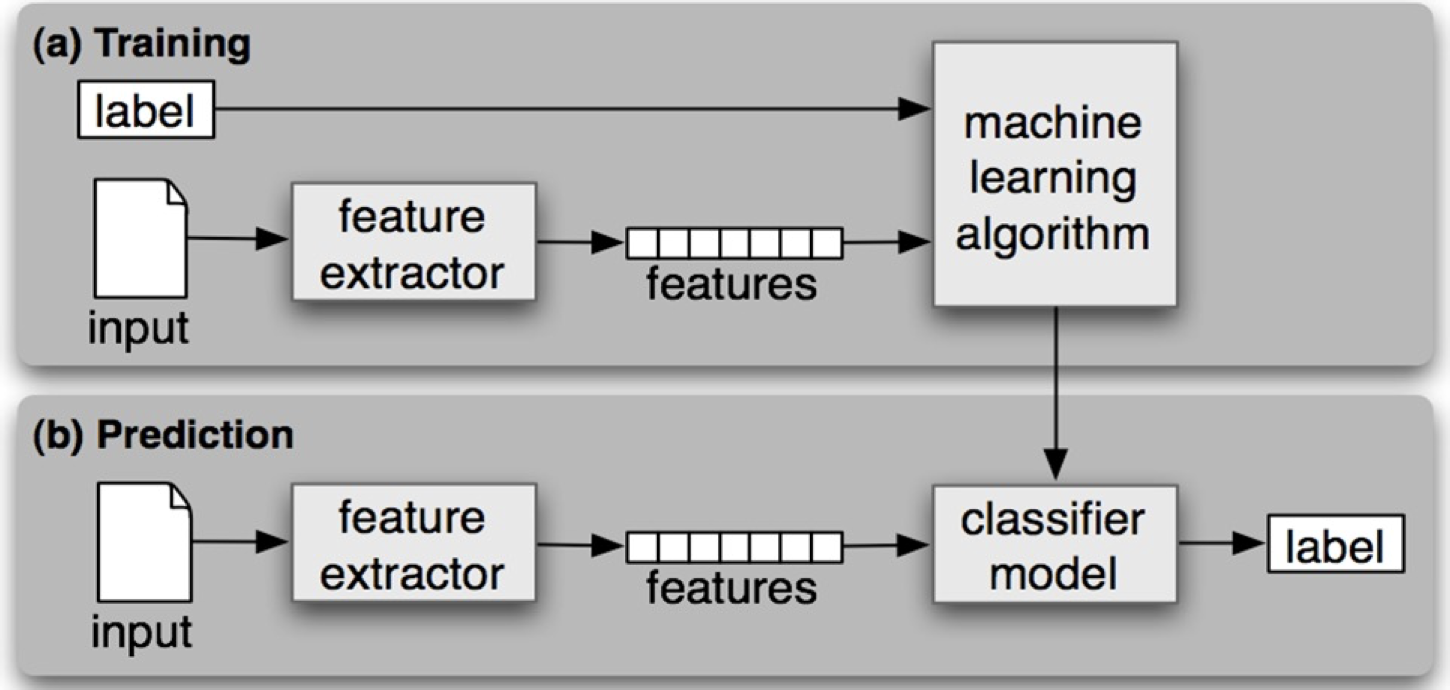
特征工程
特征:数据集中,一列一列的数据为特征;模型训练中,对预测结果有用的叫特征。
特征工程:利用专业背景知识和技巧处理数据,让机器学习算法效果最好。
特征工程是机器学习周期中最困难、最耗时的任务,需要专业知识。
数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已。
特征提取
从原始任务中提取和任务相关的特征,构成特征向量。

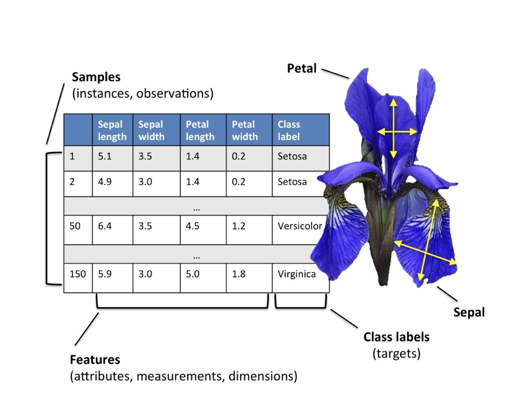
特征预处理
特征会影响模型。因量纲问题,有些特征对模型影响大,有些影响小。如通过一个人的身高和体重预测这个人的健康状况,如果身高的单位是cm和m,对模型的影响就不一样。
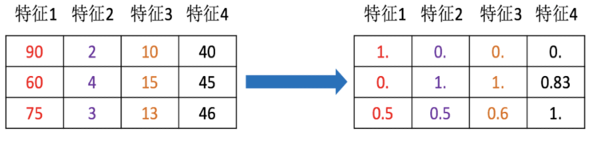
将不同的单位的特征数据转换成同一个范围内,使训练数据中不同特征对模型产生较为一致的影响。
特征降维
将原始数据的维度降低,叫做特征降维。
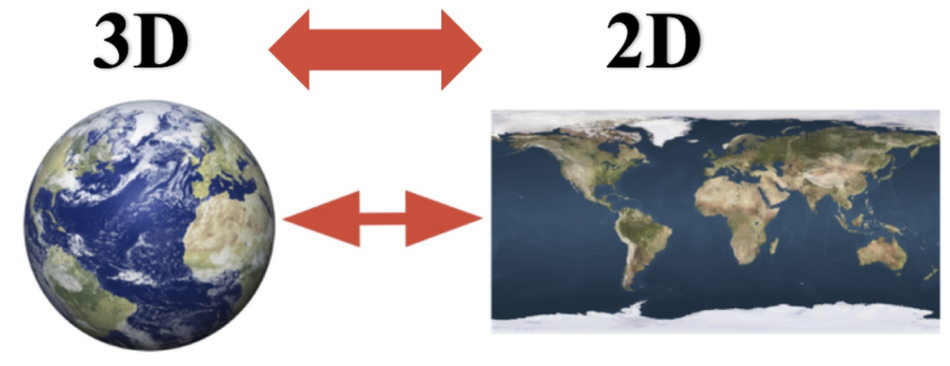
降维会丢失部分信息,降维就需要保证数据的主要信息要保留下来。原始数据会发生变化,不需要了解数据本身是什么含义,它保留了最主要的信息。
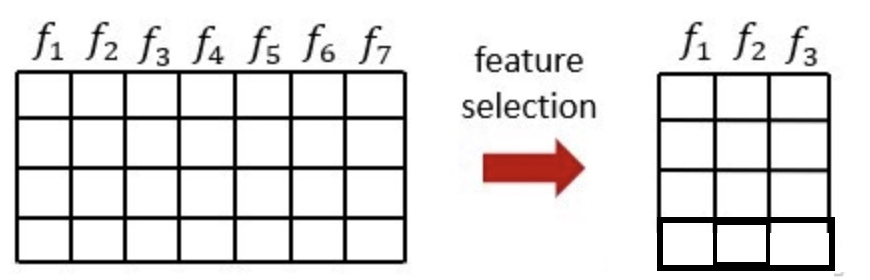
从特征中选择出一些重要特征(选择就需要根据一些指标来选择),特征选择不会改变原来的数据。
模型拟合
在机器学习或统计建模中,通过已有数据去“训练”一个数学模型,使模型参数被确定下来,从而让模型输出尽可能接近真实结果的过程。
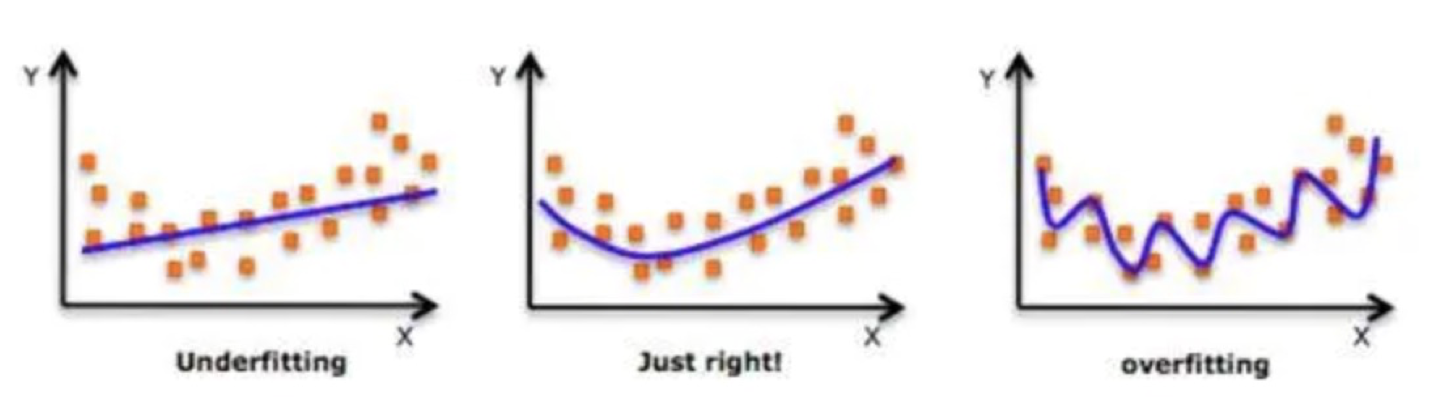
如果模型对训练集理解好,测试集理解也好,能泛化到新数据,就称为拟合良好。
如果模型对训练集和测试集理解都不好,就称为欠拟合,比如用一条直线去拟合明显弯曲的数据。
如果模型对测试集理解良好,但是测试集理解不好,就称为过拟合,好像把每个训练点都“死记硬背”。
| 维度 | 拟合良好(Good Fit) | 过拟合(Overfitting) | 欠拟合(Underfitting) |
|---|---|---|---|
| 基本定义 | 模型正确捕捉主要规律 | 模型把噪声也当成规律 | 模型没有学到有效规律 |
| 训练集误差 | 低 | 很低 | 高 |
| 测试集误差 | 低 | 高 | 高 |
| 泛化能力 | 强 | 弱 | 弱 |
| 模型复杂度 | 合适 | 过高 | 过低 |
| 对数据模式 | 抓住趋势 | 记住细节 | 忽略结构 |
| 曲线形态类比 | 平滑贴合趋势 | 过度弯曲抖动 | 过于简单僵直 |
| 是否学习噪声 | 不会 | 会 | 基本没学到 |
| 常见原因 | 特征与模型匹配 | 参数太多、模型太复杂、数据少 | 模型太简单、特征不足 |
| 训练时表现 | 稳定收敛 | 训练效果极好 | 训练效果也不好 |
| 新数据表现 | 稳定 | 明显变差 | 依旧很差 |
| 典型例子 | 合理阶数的回归曲线 | 高阶多项式强行穿点 | 用直线拟合非线性关系 |
| 改进方向 | 保持或微调 | 降复杂度、加正则、加数据 | 增复杂度、加特征、延长训练 |
scikit-learn
基于 Python 的 scikit-learn 库是机器学习的库之一,特点:
- 简单高效的数据挖掘和数据分析工具;
- 可供大家使用,可在各种环境中重复使用;
- 建立在 NumPy,SciPy 和 matplotlib 上;
- 开源,可商业使用-获取 BSD 许可证。
安装:pip install scikit-learn
KNN 算法
KNN 算法,K Nearest Neighbor,简称 KNN。思想是使用 K 个临近的样本,这些样本与待测样本最相似。若这些样本中大多数属于某一个类别,那么待测样本也属于这个类别。
KNN 算法举例
| 序号 | 电影名称 | 搞笑镜头 | 拥抱镜头 | 打斗镜头 | 电影类型 |
|---|---|---|---|---|---|
| 1 | 功夫熊猫 | 39 | 0 | 31 | 喜剧片 |
| 2 | 叶问3 | 3 | 2 | 65 | 动作片 |
| 3 | 伦敦陷落 | 2 | 3 | 55 | 动作片 |
| 4 | 代理情人 | 9 | 38 | 2 | 爱情片 |
| 5 | 新步步惊心 | 8 | 34 | 17 | 爱情片 |
| 6 | 谍影重重 | 5 | 2 | 57 | 动作片 |
| 7 | 功夫熊猫 | 39 | 0 | 31 | 喜剧片 |
| 8 | 美人鱼 | 21 | 17 | 5 | 喜剧片 |
| 9 | 宝贝当家 | 45 | 2 | 9 | 喜剧片 |
| 10 | 唐人街探案 | 23 | 3 | 17 | ? |
我们计算唐人街探案到每个样本间的欧式距离:
| 序号 | 电影名称 | 搞笑镜头 | 拥抱镜头 | 打斗镜头 | 电影类型 | 距离 | K=5时 |
|---|---|---|---|---|---|---|---|
| 1 | 功夫熊猫 | 39 | 0 | 31 | 喜剧片 | 21.47 | ✅️ |
| 2 | 叶问3 | 3 | 2 | 65 | 动作片 | 52.01 | |
| 3 | 伦敦陷落 | 2 | 3 | 55 | 动作片 | 43.42 | |
| 4 | 代理情人 | 9 | 38 | 2 | 爱情片 | 40.57 | |
| 5 | 新步步惊心 | 8 | 34 | 17 | 爱情片 | 34.44 | ✅️ |
| 6 | 谍影重重 | 5 | 2 | 57 | 动作片 | 43.87 | |
| 7 | 功夫熊猫 | 39 | 0 | 31 | 喜剧片 | 21.47 | ✅️ |
| 8 | 美人鱼 | 21 | 17 | 5 | 喜剧片 | 18.55 | ✅️ |
| 9 | 宝贝当家 | 45 | 2 | 9 | 喜剧片 | 23.43 | ✅️ |
| 10 | 唐人街探案 | 23 | 3 | 17 | ? | —— | ? |
欧式距离,就是两点间距离公式:
若两点在一维空间内:
d=∣x−y∣
若两点在二维空间内:
d=(x1−y1)2+(x2−y2)2
若两点在 n 维空间内:
d(x,y)=i=1∑n(xi−yi)2
其中:
- x=(x1,x2,…,xn)
- y=(y1,y2,…,yn)
- n 为特征维度
- d 为欧式距离
计算出待测数据和每个样本的所有距离,可以得到 5 个带有绿色对号标记的最相似样本。在这五个样本里面,有一个是爱情片,其他都是喜剧片,因此可以得出,唐人街探案为喜剧片。
K 值的选择
在上述示例中,K 值选择 5,即选择 5 个最临近的样本。
如果 K 值过小,相当于用较小领域的训练实例预测,容易受到异常点的影响,让整体模型变得复杂,容易发生过。
如果 K 值过大,相当于用较大领域的训练实例预测,会受到样本均衡的问题,且 K 值的增大就意味着整体的模型变得简单,容易发生欠拟合。
若 K=N,即 K 值等于样本训练的个数,则无论输入实例是什么,只会按训练集中最多的类别进行预测,会受到样本均衡的影响。
可通过交叉验证、网格搜索等方法调优此参数。
KNN 在分类和回归中的应用
特征空间:把样本用“特征向量”表示后,所有样本点所处的数学空间。它是由特征维度构成的坐标空间,每个样本在这个空间中都是一个点。
若一个样本在特征空间中的 k 个最相似的样本大多数属于某一个类别,则该样本也属于这个类别。样本间的相似性用欧氏距离计算,处理流程:
分类应用
- 计算未知样本到每一个训练样本的距离;
- 将训练样本根据距离大小升序排列;
- 取出距离最近的 k 个样本;
- 进行投票,统计 k 个样本中哪个类别的样本个数最多;
- 将未知的样本归属到出现次数最多的类别。
回归应用
- 计算未知样本到每一个训练样本的距离;
- 将训练样本根据距离大小升序排列;
- 取出距离最近的 K 个训练样本;
- 把这个 K 个样本的目标值计算其平均值;
- 作为将未知的样本预测的值。
使用 scikit-learn 和 KNN 计算
分类
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)n_neighbors:查询默认使用的邻居数,即 KNN 算法中的 "K"。
# 用电影的例子
from pandas import DataFrame
from sklearn.neighbors import KNeighborsClassifier
x_train = DataFrame([[39, 0, 31], [3, 2, 65], [2, 3, 55], [9, 38, 2], [8, 34, 17], [5, 2, 57], [39, 0, 31], [21, 17, 5], [45, 2, 9]])
y_train = (["喜剧片", "动作片", "动作片", "爱情片", "爱情片", "动作片", "喜剧片", "喜剧片", "喜剧片"])
x_test = DataFrame([[23, 3, 17]])
model = KNeighborsClassifier()
model.fit(x_train, y_train)
y_predict = model.predict(x_test)
print(y_predict) # ["喜剧片"]代码步骤:先导入包,然后准备数据,接着实例化模型,然后训练模型,最后预测结果。
因为一个样本可能具有多个特征,所以 x_train 和 x_test 都要用双层列表。
[39, 0, 31]是一个样本,39、3、2 等是一个特征,“喜剧片”、“动作片”等是标签,x_test 为测试集,这里测试集只有一个,所以用[[23, 3, 17]]。>>> X = [[0], [1], [2], [3]] >>> y = [0, 0, 1, 1] >>> from sklearn.neighbors import KNeighborsClassifier >>> neigh = KNeighborsClassifier(n_neighbors=3) >>> neigh.fit(X, y) KNeighborsClassifier(...) >>> print(neigh.predict([[1.1]])) [0] >>> print(neigh.predict_proba([[0.9]])) [[0.666 0.333]]
回归
sklearn.neighbors.KNeighborsRegressor(n_neighbors=5)Classfier 表示分类,Regressor 表示回归。
# 电影票房预测
from pandas import DataFrame
from sklearn.neighbors import KNeighborsRegressor
# 特征:著名演员个数、片长、煽情片段个数
x_train = DataFrame([[5, 130, 6], [2, 95, 1], [3, 110, 2], [6, 145, 8], [4, 120, 4], [1, 90, 0], [7, 150, 9], [3, 105, 3]])
y_train = [980, 320, 450, 1200, 760, 210, 1500, 520]
x_test = DataFrame([[4, 125, 5]])
model = KNeighborsRegressor(n_neighbors=3)
model.fit(x_train, y_train)
y_predict = model.predict(x_test)
print("预测票房(百万):", y_predict) # [730.]距离度量方法
欧式距离
欧氏距离是最常用的一种距离度量方式,用于衡量两个点在欧几里得空间中的直线距离。直观理解:就是几何中“两点之间线段的长度”。
在 n 维空间中,点 x=(x1,x2,…,xn) 和 y=(y1,y2,…,yn) 之间的欧式距离为:
d(x,y)=i=1∑n(xi−yi)2
曼哈顿距离
也成为“城市街区距离”,源于曼哈顿城市街区横平竖直的特点。
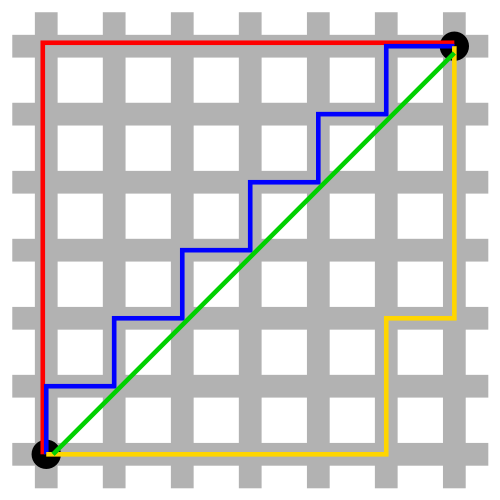
曼哈顿与欧几里得距离:红、蓝与黄线分别表示所有曼哈顿距离都拥有一样长度(12),而绿线表示欧几里得距离有 6×2≈8.48 的长度。
在 n 维空间中,点 x=(x1,x2,…,xn) 和 y=(y1,y2,…,yn) 之间的曼哈顿距离为:
d=i=1∑n∣ai−bi∣
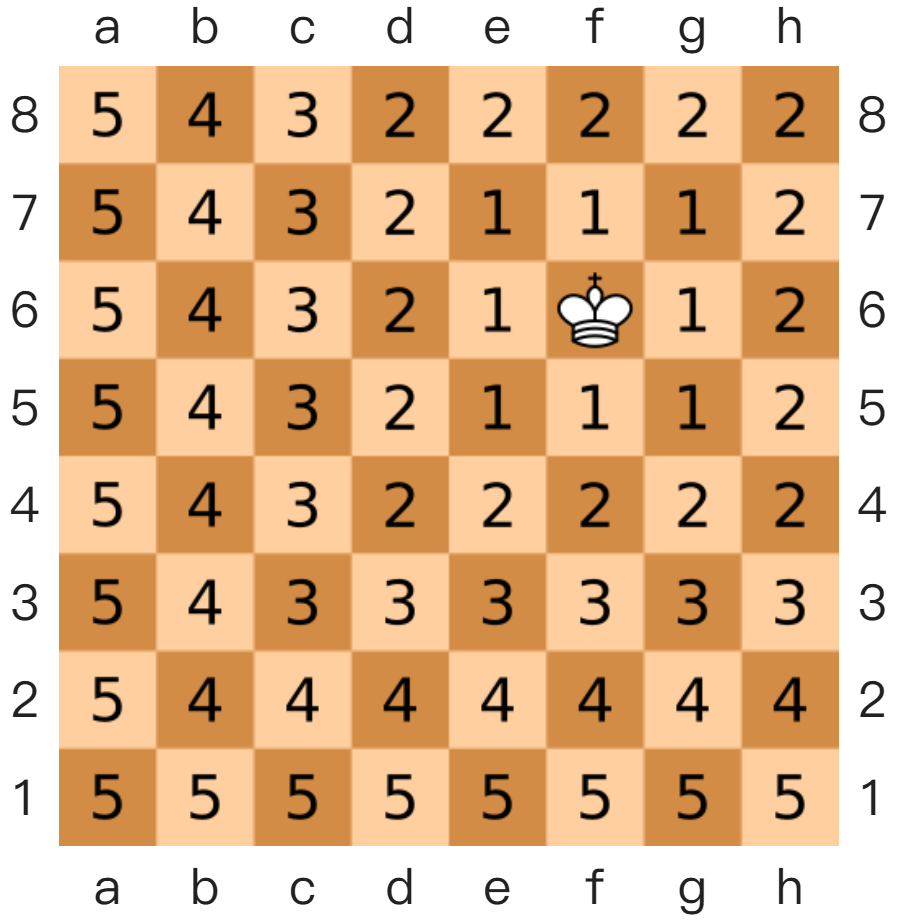
切比雪夫距离
国际象棋中,国王可以执行、横行、斜行,所以国王走一步可以移动到相邻 8 个方格中的任意一个。国王从格子 (x1,y1) 走到格子 (x2,y2) 走过的最少步数就是切比雪夫距离。
闵式距离
闵可夫斯基距离,不是一种新的距离的度量方式,而是距离的组合,是对多个距离度量公式的概括性的表述。
两个 n 维变量 (a1,a2,…,an) 和 (b1,b2,…,bn) 间的闵可夫斯基距离定义为:
d=ni=1∑n∣ai−bi∣p
其中 p 是一个变参数:
- p=1 时,此公式就是曼哈顿距离;
- p=2 时,此公式就是欧氏距离;
- p→∞ 时,此公式就是切比雪夫距离。
根据 p 的不同,闵式距离可表示某一类种的距离。
特征预处理
如果不同特征间量纲不同,取值范围有差异,容易影响目标检测的结果,模型(算法)会无法学到其他特征。
量纲:量纲是用来描述一个物理量或数值所依赖的基本单位类型,用于说明“这个量本质上属于什么类别”。
| 编号 | 身高(m) | 体重(kg) | 视力(0.2–2.0) | 健康状况 |
|---|---|---|---|---|
| 1 | 1.70 | 67 | 1.5 | 1 |
| 2 | 1.71 | 80 | 0.8 | 2 |
| 3 | 1.75 | 70 | 1.5 | 1 |
| 4 | 1.76 | 68 | 1.2 | 1 |
| 5 | 1.80 | 80 | 1.8 | 1 |
| 6 | 1.81 | 90 | 0.6 | 2 |
上个表格中,体重的单位是kg,对模型的预测影响很大,需要处理。
这里介绍两种常用的特征缩放方法,归一化和标准化。
归一化
思想是将原始数据变换为 [xmin,xmax] 之间,默认是 [0,1]。
若映射范围是 [0,1],公式为 x′=xmax−xminx−xmin,如果自定义范围 [Xmin,Xmax],则公式为 X′′=X′⋅(n−m)+m。
通过 sklearn 实现:
sklearn.preprocessing.MinMaxScaler(feature_range=(0, 1))feature_range: 缩放区间,默认是 [0,1]。
此方法返回一个 MinMaxScaler 对象,使用这个对象的 fit_transform(data) 就可以对数据集进行归一化操作。
# 导包
from sklearn.preprocessing import MinMaxScaler # 归一化对象
# 1. 准备数据集(归一化之前的原数据).
x_train = [[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]]
# 2. 创建归一化对象.
# 参数feature_range 表示生成范围, 默认为: 0, 1 如果就是这个区间, 则参数可以省略不写.
transfer = MinMaxScaler()
# transfer = MinMaxScaler(feature_range=(3, 5))
# 3. 对原数据集进行归一化操作.
x_train_new = transfer.fit_transform(x_train)
# 4. 打印处理后的数据.
print("归一化后的数据集为: \n")
print(x_train_new)
# 归一化后的数据集为:
# [[1. 0. 0. 0. ]
# [0. 1. 1. 0.83333333]
# [0.5 0.5 0.6 1. ]]归一化受到最大值与最小值的影响,这种方法容易受到异常数据的影响,鲁棒性较差,适合传统精确小数据场景。
鲁棒性:鲁棒性指系统、模型或算法在存在噪声、异常、扰动或不确定性的情况下,仍能保持稳定性能和合理输出的能力。
标准化
通过对原始数据进行标准化,将数据转换为均值为 0 标准差为 1 的标准正态分布的数据。
公式:X′=σx−xˉ,其中 xˉ 为样本平均值,也可用 mean 代替;σ 为样本标准差。
通过 sklearn 实现:
sklearn.preprocessing.StandardScaler()此方法返回一个 StandardScaler 对象,和 MinMaxScaler 一样,使用 fit_transform(data) 就可以处理数据。
# 1.导入工具包
from sklearn.preprocessing import StandardScaler
# 2.数据(只有特征)
x = [[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]]
# 3.实例化
process = StandardScaler()
# 4.fit_transform 处理
data = process.fit_transform(x)
# print(data)
print(process.mean_) # [75. 3. 12.66666667 43.66666667]
print(process.var_) # [150. 0.66666667 4.22222222 6.88888889]对于标准化来说,如果出现异常点,由于具有一定数据量,少量的异常点对于平均值的影响并不大。现代的机器学习场景中,数据集的规模会很大,我们多使用标准化处理数据,而不使用归一化。
使用 KNN 算法对鸢尾花分类
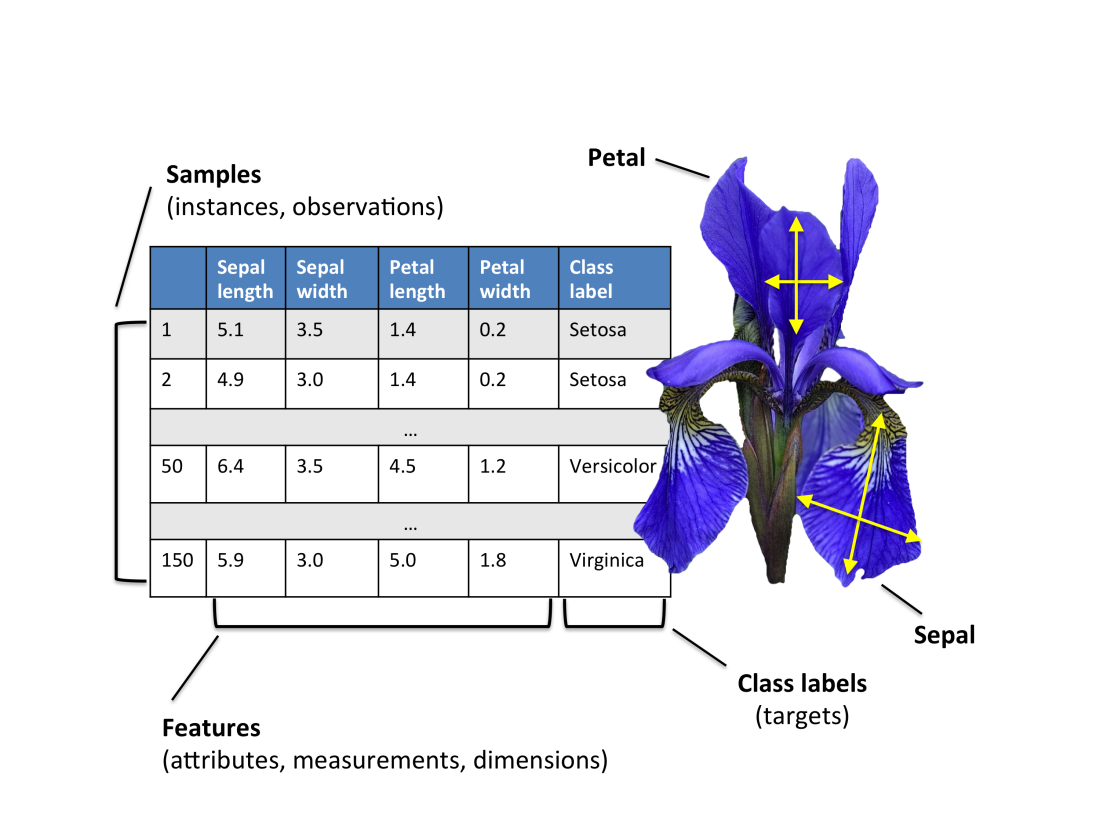
莺尾花数据集介绍
鸢尾花数据集是机器学习中最经典的入门数据集之一,常用于:分类算法演示、聚类算法演示、特征分析练习、可视化教学,属于监督学习中的多分类数据集。
它有四个特征字段:
| 特征名 | 含义 | 单位 |
|---|---|---|
| sepal length | 花萼长度 | cm |
| sepal width | 花萼宽度 | cm |
| petal length | 花瓣长度 | cm |
| petal width | 花瓣宽度 | cm |
有三个标签类别:
| 类别编号 | 类别名 |
|---|---|
| 0 | setosa(山鸢尾) |
| 1 | versicolor(变色鸢尾) |
| 2 | virginica(维吉尼亚鸢尾) |

from sklearn.datasets import load_iris
dataset = load_iris()
print(f"查看数据集的前5行数据: \n{dataset.data[:5]}\n")
print(f"查看数据集的特征名称: {dataset.feature_names}\n")
print(f"查看数据集的标签名称: {dataset.target_names}\n")
print(f"查看数据集的标签值: \n{dataset.target}\n")
# print(f"查看数据集的描述信息: \n{dataset.DESCR}\n")
print(f"查看数据集的文件名: {dataset.filename}")查看数据集的前5行数据:
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]
查看数据集的特征名称: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
查看数据集的标签名称: ['setosa' 'versicolor' 'virginica']
查看数据集的标签值:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
查看数据集的文件名: iris.csv莺尾花数据集可视化
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns # 用于可视化
from sklearn.datasets import load_iris
plt.rcParams["font.family"] = ["Times New Roman", "SimSun"] # 英文字体为新罗马,中文字体为宋体
plt.rcParams["font.serif"] = ["Times New Roman", "SimSun"] # 衬线字体
plt.rcParams["font.sans-serif"] = ["Times New Roman", "SimSun", "Arial", "SimHei"] # 无衬线字体,与Latex相关
plt.rcParams["mathtext.fontset"] = "custom" # 设置LaTeX字体为用户自定义,这里演示,就不用computer modern了
plt.rcParams["axes.unicode_minus"] = False
dataset = load_iris()
df = pd.DataFrame(dataset.data, columns=dataset.feature_names)
df["target"] = dataset.target
sns.lmplot(data=df, x="sepal length (cm)", y="sepal width (cm)", hue="target") # 绘制散点图
# plt.tight_layout()
plt.title("莺尾花数据集可视化")
plt.show()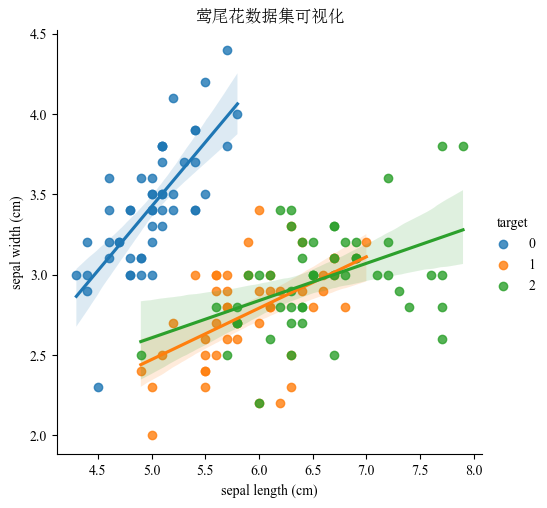
分割数据集
将数据集分为测试集和数据集,要使用到sklearn.model_selection.train_test_split函数。
def train_test_split(*arrays,
test_size=None,
train_size=None,
random_state=None,
shuffle=None) -> List:
...arrays: 要分割的数据,可以是 Python 列表、Numpy 数组、Scipy-Sparse矩阵、Pandas DataFrame。test_size: 测试集数量,如果是浮点数,则表示测试集的占比;如果是整数,则代表测试集的数量。train_size: 训练集数量,如果是浮点数,则表示训练集的占比;如果是整数,则代表训练集的数量。random_state: 随机种子,如果种子一致,生成的随机数一致,那么分割的结果也一致。shuffle: 是否打乱。
返回值跟 *arrays 参数有关。如果传入的是 train_test_split(A1, A2, A3, ..., AN),返回值就是 A1_train, A1_test, A2_train, A2_test, A3_train, A3_test, ..., AN_train, AN_test。
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
dataset = load_iris()
print(f"数据集的类型为: {type(dataset.data)}") # <class 'numpy.ndarray'>
# 拆分数据集
x_train, x_test, y_train, y_test = train_test_split(dataset.data, dataset.target, test_size=0.2)
print(f"{len(x_train)=}, {len(x_test)=}, {len(y_train)=}, {len(y_test)=}")
# len(x_train)=120, len(x_test)=30, len(y_train)=120, len(y_test)=30模型训练
使用 sklearn.neighbors.KNeighborsClassifier 训练模型,并预测自定义数据。
from sklearn.datasets import load_iris # 加载鸢尾花测试集的
from sklearn.model_selection import train_test_split # 分割训练集和测试集的
from sklearn.preprocessing import StandardScaler # 数据标准化的
from sklearn.neighbors import KNeighborsClassifier # KNN算法 分类对象
from sklearn.metrics import accuracy_score # 模型评估的, 计算模型预测的准确率
iris_data = load_iris()
# 2. 数据的预处理, 这里是把150条数据, 按照 8:2的比例, 切分训练集和测试集.
x_train, x_test, y_train, y_test = train_test_split(iris_data.data, iris_data.target, test_size=0.2, random_state=23)
# 3. 特征工程(提取, 预处理...)
# 思考1: 特征提取: 因为源数据只有4个特征列, 且都是我们用的, 所以这里无需做特征提取.
# 思考2: 特征预处理: 因为源数据的4列特征差值不大, 所以我们无需做特征预处理, 但是, 加入特征预处理会让我们的代码更完善, 所以加入.
# 3.1 创建标准化对象.
transfer = StandardScaler()
# 3.2 对特征列进行标准化, 即: x_train: 训练集的特征数据, x_test: 测试集的特征数据.
# fit_transform: 兼具fit和transform的功能, 即: 训练, 转换. 该函数适用于: 第一次进行标准化的时候使用. 一般用于处理: 训练集.
x_train = transfer.fit_transform(x_train)
# transform: 只有转换. 该函数适用于: 重复进行标准化动作时使用, 一般用于对测试集进行标准化.
x_test = transfer.transform(x_test)
# 4. 模型训练.
# 4.1 创建模型对象.
estimator = KNeighborsClassifier(n_neighbors=3)
# 4.2 具体的训练模型的动作.
estimator.fit(x_train, y_train) # 传入: 训练集的特征数据, 训练集的标签数据
# 5. 模型预测.
# 场景1: 对刚才切分的 测试集(30条) 进行测试.
# 5.1 直接预测即可, 获取到: 预测结果
y_pre = estimator.predict(x_test) # x_test: 测试集的特征数据
# 5.2 打印预测结果.
print(f"预测值为: {y_pre}")
# 场景2: 对新的数据集(源数据150条 之外的数据) 进行测试.
# 5.1 自定义测试数据集.
my_data = [[7.8, 2.1, 3.9, 1.6]]
# 5.2 对数据集进行标准化处理.
my_data = transfer.transform(my_data)
# 5.3 模型预测.
y_pre_new = estimator.predict(my_data)
print(f"预测值为: {y_pre_new}")
# 5.4 查看上述数据集, 每种分类的预测概率.
y_pre_proba = estimator.predict_proba(my_data)
print(f"(各分类)预测概率为: {y_pre_proba}") # [[0, 0.66666667, 0.33333333]] -> 0分类的概率, 1分类的概率, 2分类的概率.
# 6. 模型评估.
# 方式1: 直接评分, 基于: 测试集的特征 和 测试集集的标签.
print(f"正确率(准确率): {estimator.score(x_test, y_test)}") # 0.9666666666666667
# 方式2: 基于 测试集的标签 和 预测结果 进行评分.
print(f"正确率(准确率): {accuracy_score(y_test, y_pre)}") # 0.9666666666666667预测值为: [2 2 1 0 2 1 0 2 0 1 1 0 2 0 0 1 1 1 2 0 2 0 0 0 2 0 0 2 1 1]
预测值为: [1]
(各分类)预测概率为: [[0. 0.66666667 0.33333333]]
正确率(准确率): 0.9666666666666667
正确率(准确率): 0.9666666666666667常见问题
为什么模型在做标准化的时候先使用 fit_transform(),后使用 transform()?
模型标准化的公式为:X′=σx−xˉ,这里需要一个 xˉ、σ,都需要从样本的数据中计算得出。在 sklearn 中,这些参数通过 StandardScaler 对象的 fit() 方法得出,内部会得到 mean_ 和 std_ 这两个值。transform() 方法是在 fit() 的基础上做运算,如果不先 fit(),会报错。fit_transform() 方法就是先 fit(),并将参数保存到对象内,再 transform()。
测试集必须只用 transform(),防止数据泄露。否则模型会“偷看数据”,导致测试集均值/方差被重新计算、测试集信息参与了参数生成,评估结果会被污染,泛化能力评估失真。
版权所有
版权归属:棋
